EXERCICE 1 :
EXERCICE 2 :
1. a) = la probabilité que le résultat soit égal à 2 sachant qu’il est inférieur ou égal à 4.
b)= la probabilité que le résultat soit impair sachant qu’il n’est pas égal à 2.
2. a) = la probabilité que le résultat soit pair sachant qu’il est inférieur ou égal à 4.
b) P(C|A) = la probabilité que le résultat soit inférieur ou égal à 4 sachant qu’il est pair.
On a :
–
(car il y a 4 résultats possibles inférieurs ou égaux à 4 sur les 6 résultats possibles au total).
(il y a 2 résultats possibles qui sont pairs et inférieurs ou égaux à 4).
Donc .
(car il y a 3 résultats possibles qui sont pairs sur les 6 résultats possibles au total).
(il y a 2 résultats possibles qui sont pairs et conformes aux programmes actuels).
Donc .
EXERCICE 3 :
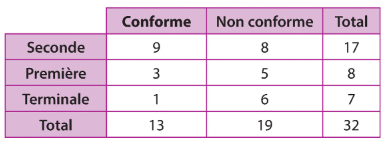
1.
2. = la probabilité que le manuel soit conforme sachant que c’est un manuel de Terminale.
On a , car il y a 4 manuels de Terminale conformes.
P(T) = 1/8.
Donc .
3. = la probabilité que le manuel soit conforme sachant que ce n’est pas un manuel de Seconde.
On a , car il y a 12 manuels qui sont conformes et qui ne sont pas des manuels de Seconde.
.
Donc
.
= la probabilité que ce ne soit pas un manuel de Seconde sachant qu’il est conforme.
On a , car il y a 12 manuels qui sont conformes et qui ne sont pas des manuels de Seconde.
p(C) = 7/8.
Donc
.
EXERCICE 4 :
1. L’arbre pondéré de la situation est le suivant :
Créer l’arbre…..
2. La probabilité qu’il achète un poivron jaune bio correspond à la probabilité de l’événement J ∩ B, soit :
3. On calcule tout d’abord :
On en déduit ensuite :
EXERCICE 5 :
1. L’arbre pondéré de la situation est le suivant :
Tracer l’arbre pondéré….
2. La probabilité de l’événement correspond à :
3. On calcule tout d’abord :
On en déduit ensuite :
4. On calcule tout d’abord :
On en déduit ensuite :
5. Pour savoir si Sophie doit plutôt choisir une dragée bleue ou rose, il faut comparer les probabilités conditionnelles et
.
Donc si Sophie préfère les dragées contenant une amande, elle doit plutôt choisir une dragée rose.
EXERCICE 6 :
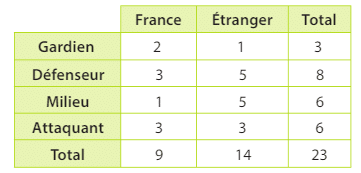
1. On calcule tout d’abord p(G) :
p(G) = 2/23
On calcule ensuite p(F) :
p(F) = 10/23
2. On calcule tout d’abord :
On calcule ensuite :
On calcule enfin :
3. On calcule tout d’abord :
On calcule ensuite :
4. On calcule tout d’abord p(G ∩ M) :
p(G ∩ M) = 2/23
On calcule ensuite p(M) :
p(M) = 8/23
On en déduit enfin p_G(M) :
5. On cherche une probabilité conditionnelle égale à 5/8.
Étant donné qu’il n’y a pas de résultat de ce type évident à obtenir, on peut chercher une combinaison de probabilités conditionnelles qui peut donner cette valeur.
Par exemple, on peut chercher sachant que
et
. On sait que :
= p(A ∩ G ∩ F) / p(F)
On peut donc développer cette expression :
= p(F|G ∩ A) × p(A|G) × p(G) / p(F)
= p(F|A ∩ G) × p(A|G) × p(G) / (p(F|A ∩ G) × p(A|G) × p(G) + p(F|
∩ G) × p(
|G) × p(G))
En insérant les valeurs numériques connues, on trouve :
6. On calcule tout d’abord p(G ∪ D) :
p(G ∪ D) = 7/23
On calcule ensuite :
EXERCICE 7 :
1. On peut penser que la répétition de cette épreuve deux soirs consécutifs est une succession de deux épreuves indépendantes car la présence de courrier ou non un soir n’affecte pas la présence ou non de courrier le soir suivant.
2. L’arbre pondéré pour cette succession de deux épreuves indépendantes est le suivant :
Tracer l’arbre pondéré….
3. Le tableau à double entrée pour cette succession de deux épreuves indépendantes est le suivant :
Tracer l’arbre pondéré….
EXERCICE 8 :
1. On peut penser que ces deux tirages sont une succession de deux épreuves indépendantes car la pièce choisie par Ornella dans sa poche ne dépend pas de celle choisie par Fanny dans son porte-monnaie.
2. L’arbre pondéré pour cette succession de deux épreuves indépendantes est le suivant :
Tracer l’arbre pondéré….
3. Le tableau à double entrée pour cette succession de deux épreuves indépendantes est le suivant :
Tracer l’arbre pondéré….
EXERCICE 10 :
La répartition des défauts est :
• 14 % d’équerres défectueuses;
• 30 % de rapporteurs sans défaut;
• 70 % d’équerres.
• 30 % de rapporteurs.
L’arbre pondéré pour cette situation est le suivant :
Tracer l’arbre pondéré….
Les événements sur cet arbre correspondent à :
• E : le matériel produit est une équerre;
• D : le matériel produit est défectueux;
• R : le matériel produit est un rapporteur;
• S : le matériel produit est sans défaut.
EXERCICE 11 :
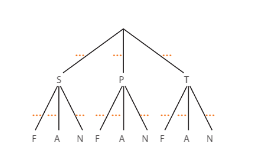
1. L’arbre pondéré pour cette situation est le suivant :
Tracer l’arbre pondéré….
Les événements sur cet arbre correspondent à :
• S : l’élève est en seconde;
• P : l’élève est en première;
• T : l’élève est en terminale;
• F : l’élève pratique le football;
• A : l’élève pratique l’athlétisme;
• N : l’élève pratique la natation.
2.
a)
b)
c)
3. On peut utiliser les probabilités conditionnelles pour déterminer la probabilité qu’un élève soit en seconde, première ou terminale sachant qu’il se rend à la piscine pour faire de la natation. On cherche à comparer les quantités p(S|N), p(P|N) et p(T|N).
On sait que :
p(S|N) = p(N|S) × p(S) / p(N)
p(P|N) = p(N|P) × p(P) / p(N)
p(T|N) = p(N|T) × p(T) / p(N)
En insérant les valeurs numériques connues, on trouve :
p(S|N) ≈ 0,349
p(P|N) ≈ 0,27
p(T|N) ≈ 0,382
Il est donc plus probable que l’élève soit en terminale s’il se rend à la piscine pour faire de la natation.
4.
a) On a :
p(A ∪ N) = p(A) + p(N) – p(A ∩ N)
p(A ∩ N) = p(S) × p(A|S) × p(N|S) + p(P) × p(A|P) × p(N|P) + p(T) × p(A|T) × p(N|T)
p(A ∩ N) = 0,24 × 0,12 × 0,43 + 0,61 × 0,34 × 0,22 + 0,15 × 0,09 × 0,5 ≈ 0,03246
p(A ∪ N) ≈ 0,12 + 0,123145 – 0,03246 ≈ 0,210685
b) On cherche à calculer la probabilité que l’élève soit en seconde ou qu’il fasse du football. On a :
p(S ∪ F) = p(S) + p(F) – p(S ∩ F)
p(S ∩ F) = p(S) × p(F|S) = 0,24 × 0,12 = 0,0288
p(S ∪ F) = 0,24 + 0,12 – 0,0288 = 0,3312
EXERCICE 12 :
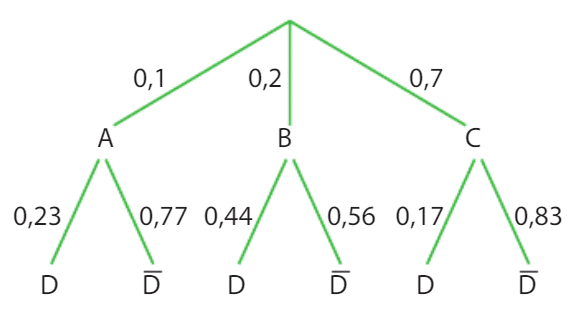
1.
Tracer l’arbre pondéré….
2. On calcule les probabilités :
*
*
*
On remarque que
Puis on calcule
Et
Comme , les événements A et C sont indépendants.
EXERCICE 13 :
On sait que la proportion de filles en terminale est de . Donc la probabilité que l’élève soit une fille en terminale est de
.
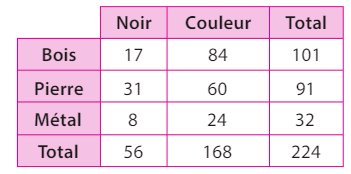
EXERCICE 14 :
Les probabilités conditionnelles sont :
On calcule
et
Comme P(F/T) = P(F), les événements F et T sont indépendants si et seulement si P(F/T) = P(F), soit 6/n = 6/(16n+63), ce qui donne n = 21.
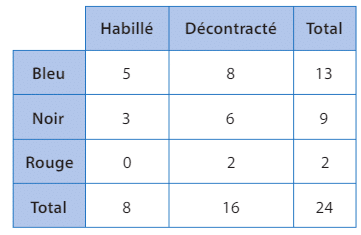
1. Les probabilités sont :
a)
b)
c)
2. Les événements N et M sont indépendants si et seulement si P(N/M) = P(N), soit .
Ce n’est pas le cas, donc les événements N et M ne sont pas indépendants.
3. Les événements N et B sont indépendants si et seulement si P(N/B) = P(N), soit.
Ce n’est pas le cas, donc les événements N et B ne sont pas indépendants.
EXERCICE 15 :
1.
Tracer l’arbre pondéré….
2.
a) On calcule
et .
Donc les événements S et M sont indépendants car .
b) On calcule .
On remarque que , donc les événements S et M ne sont pas indépendants.
c) On utilise le théorème de Bayes :
.
Donc la probabilité que le poisson ait été péché par Saumonix sachant que le client est mécontent est d’environ 30,3%.
3. On note x la proportion de poisson acheté chez le grossiste normand et y la proportion de poisson acheté chez le grossiste de Paris.
On veut que la proportion de clients mécontents soit de 30%. On calcule P(M) pour cette nouvelle configuration :
On résout l’équation
pour trouver y en fonction de x :
On sait que , donc on peut trouver x :
Donc Saumonix doit acheter environ 47% de son poisson chez le grossiste normand et 53% chez le grossiste de Paris pour atteindre son objectif.
EXERCICE 16 :
La probabilité que la famille de Yannis parte Istanbul est de 0,9 et la probabilité qu’il ne pleuve pas est de 0,85.
On calcule la probabilité que les deux événements se produisent en multipliant les probabilités : .
Donc la probabilité que Yannis parte Istanbul pour ses prochaines vacances et qu’il n’y pleuve pas est d’environ 76,5%.
EXERCICE 17 :
1.
Tracer l’arbre pondéré….
2. On calcule les probabilités :
3. On utilise la formule des probabilités totales pour calculer la probabilité que Émilie doive utiliser son chalumeau :
ou encore
.
Donc la probabilité que Émilie doive utiliser son chalumeau pour cette intervention est d’environ 86,3%.
EXERCICE 18 :
1. On calcule les probabilités :
* P(A) = 0,5, P(D) = 0,25 et .
* P(B) = 0,3, P(D) = 0,25 et .
On calcule aussi , et P(C) = 0,5.
Pour savoir si A et D sont indépendants, on doit vérifier si .
Mais , donc les événements A et D ne sont pas indépendants.
Pour savoir si B et D sont indépendants, on doit vérifier si .
On a , donc les événements B et D sont indépendants.
EXERCICE 19 :
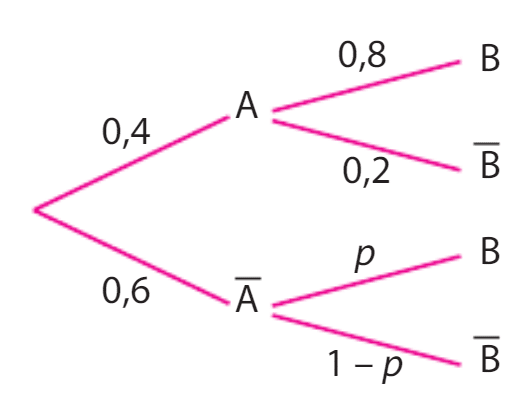
On veut que A et B soient indépendants, donc .
On calcule à partir de l’arbre :
Donc on doit avoir
.








 Mathématiques Web c'est 2 208 479 fiches de cours et d'exercices téléchargées.
Mathématiques Web c'est 2 208 479 fiches de cours et d'exercices téléchargées.