Les vecteurs et les repères à travers des exercices de maths en 2de qui vont vous aider à maîtriser ce chapitre clé. L’élève devra connaître la d’édition d’un repère cartésien orthogonal et orthonormé et savoir calculer les coordonnées et la norme d’un vecteur ou d’une distance. Vous devrez également savoir démontrer si deux vecteurs du plan sont colinéaires et donner l’équation réduite ou cartésienne d’une droite. Ces énoncés disposent de leur correction et peuvent être imprimés en PDF afin de travailler librement et de vous auto-corriger en seconde.
Exercice 1 :
Soit ABCD un trapèze convexe tel que : (AB)//(DC), AB = 5 et DC = 7.
1) a) A partir de ces hypothèses, montrer que
b) Exprimer en fonction de
et
.
2) On considère le point E tel que 5 = 2
a) Déterminer en fonction de
, puis placer E.
b) Montrer que les segments [AE] et [BD] ont même milieu.
3) A chaque réel x , on fait correspondre le point M tel que = x
+
.
a) Pour quelle valeur de x le point M est-il le symétrique de C par rapport à D ?
b) Exprimer en fonction de
. Sur quelle ligne se déplace le point M lorsque x varie ?
Exercice 2 :
Soit ABC un triangle et x un réel.
A chaque valeur de x on associe les points E et F tels que : et
1) Construire E et F pour .
2) Montrer que, pour tout x de ,
est colinéaire à
.
3) Pour quelles valeurs de x a-t-on :
a) E = F ?
b) BCFE est un parallélogramme ?
Exercice 3 :
Soit ABCD un quadrilatère, on défini les points M et N par : et
( a étant un réel)
1) Montrer que pour tout réel a , on a :
2) Que dire de MBCN si ABCD est un parallélogramme ?
Exercice 4 :
Soit un réel a et un triangle RST. Soit aussi les points M, N et U définis par
;
;
1) Placer les points M, N et U lorsque a = 0.
2) Démontrer que pour tout réel a , les vecteurs et
sont colinéaires. Que peut-on en déduire ?
3) Démontrer que pour tout réel a , SMTU est un parallélogramme
Exercice 5 :
Soit ABC un triangle.
1) On donne G tel que .
Déterminer en fonction de
et
puis construire G.
2) Soit H tel que , montrer que G est le milieu de [HC]
3) Montrer que pour tout point M, .
4) Déterminer et construire l’ensemble des points M du plan tels que :
a) .
b) est colinéaire à
.
Exercice 6 :
Recopier et compléter les égalités suivantes avec le nombre réel manquant.
Exercice 7 :
1.A partir de la figure, citer un vecteur :
a) opposé à .
b) de même direction et de même sens que .
c) de même direction que mais de sens contraire.
d) égal au vecteur .
Exercice 8 :
A partir de la figure :
- Donner les images des points C, D, E par la translation de vecteur
.
- Citer trois vecteurs égaux au vecteur
.
- Citer les trois parallélogrammes définis par les trois égalités vectorielles du 2.
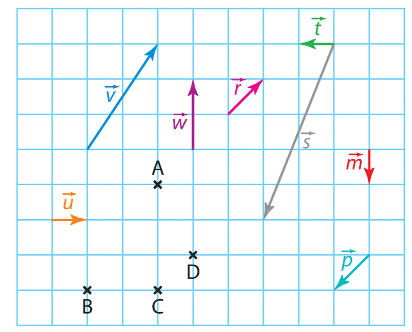
Exercice 9 :
1.Reproduire la figure ci-dessous.
2.Construire un représentant de chacun des vecteurs suivants.
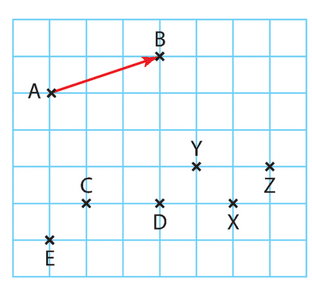
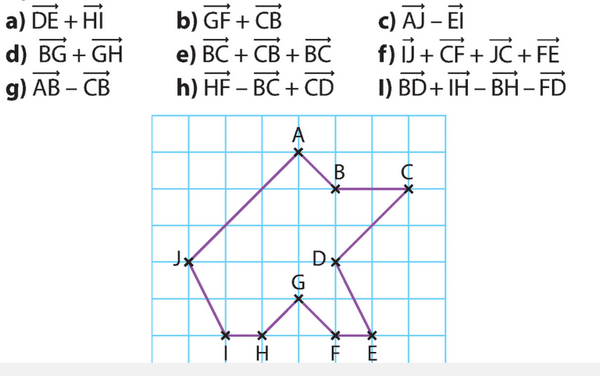
Exercice 10 :
En utilisant les points de la figure, donner un vecteur égal à :
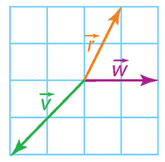
Exercice 11 :
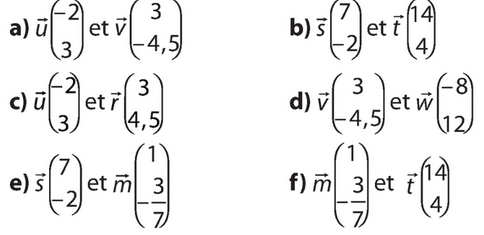
- Calculer les déterminants des vecteurs suivants.
- Dire s’ils sont colinéaires.
- S’ils sot colinéaires, trouver un coefficient de colinéarité.
Exercice 12 :
Soit trois points A, B et C distincts non alignés.
Les vecteurs et
sont-ils colinéaires dans les cas suivants ?


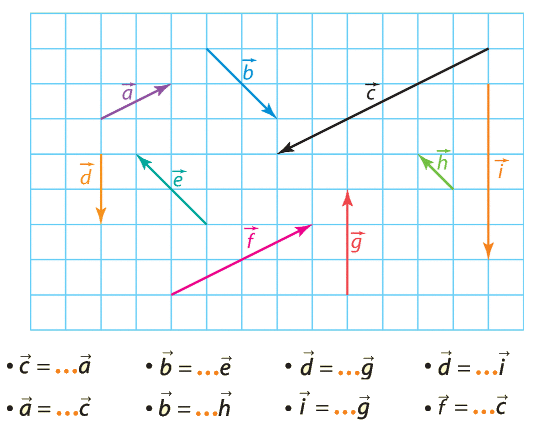
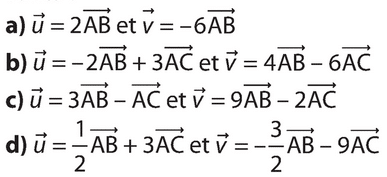



 Mathématiques Web c'est 2 207 904 fiches de cours et d'exercices téléchargées.
Mathématiques Web c'est 2 207 904 fiches de cours et d'exercices téléchargées.