sommaire
I. Division euclidienne et critères de divisibilité
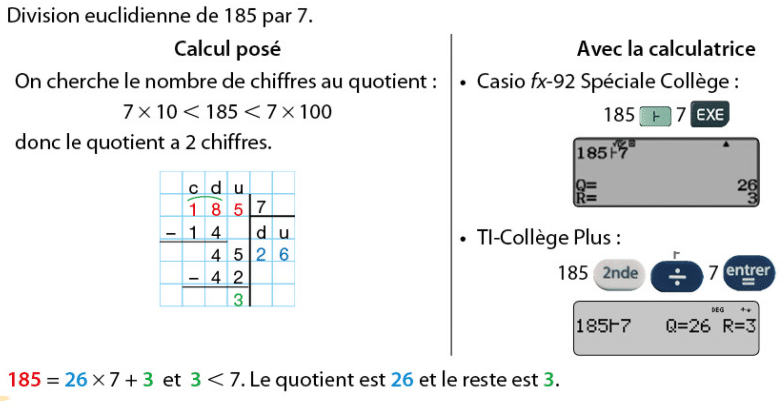
1.La division euclidienne
Effectuer la division euclidienne d’un nombre entier (le dividende) par un nombre entier (le diviseur) différent de zéro, c’est trouver deux nombres entiers, le quotient et le reste, tels que : 
avec reste < diviseur.
Exemple :
2. Multiples et diviseurs
La division euclidienne de 36 par 9 a pour reste 0.En effet : 36 = 4×9 + 0.
On dit que « 36 est un multiple de 9 », « 36 est divisible par 9″, » 9 est un diviseur de 36″.
3. Critères de divisibilité par 2, 3, 4, 5, 9 et 10
Un nombre entier est divisible par :
- 2 lorsqu’il se termine par 0,2 , 4, 6 ou 8.C’est un nombre pair;
- 3 lorsque la somme de ses chiffres est un multiple de 3;
- 4 lorsque le nombre formé par ses deux derniers chiffres est divisible par 4;
- 5 lorsqu’il se termine par 0 ou 5;
- 9 lorsque la somme de ses chiffres est un multiple de 9;
- 10 lorsqu’il se termine par 0.
Exemples :
- 240 est divisible par 2 car il se termine par 0 mais également par 5 et 10;
- 65 est divisible par 5 car il se termine par 5;
- 1 845 est divisible par 9 car 1+8+4+5=18 et 18 est un multiple de 9;
- 128 est divisible par 4 car 28 est divisible par 4 en effet .
II. La division décimale
Soit a un nombre décimal et b un nombre entier différent de zéro.
Effectuer la division décimale de a par b, c’est trouver le nombre appelé quotient
par lequel multiplier b pour obtenir a :
et .
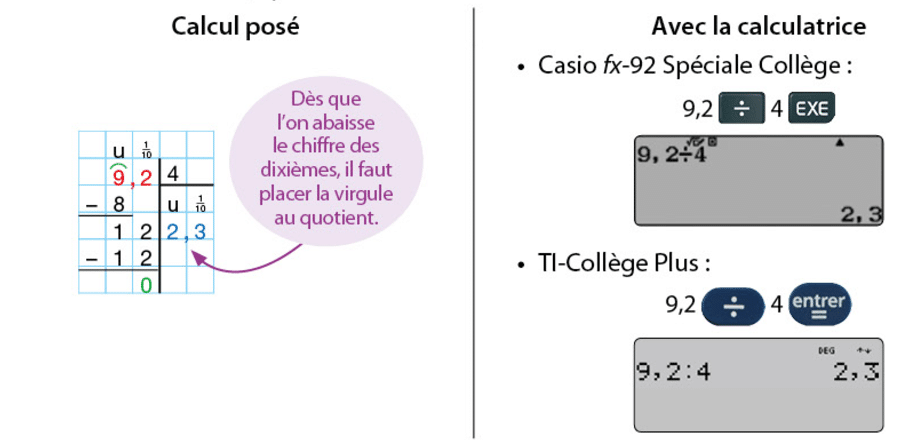
Exemple 1 :
Effectuer la division décimale de 9,2 par 4.
Le quotient de 9,2 par 4 est le nombre décimal 2,3.
Ainsi c’est à dire que .
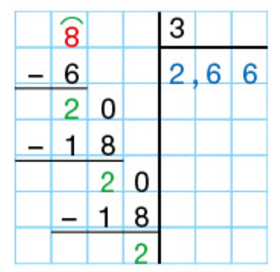
Exemple 2 :
Effectuer la division décimale de 8 par 3.
Cette division ne se termine jamais.
Le quotient de 8 par 3 n’est pas un nombre décimal.
Dans ce cas, on peut donner une valeur approchée du quotient :
- ( au dixième près).
- ( au centième près).
Avez-vous assimilé le cours sur la division euclidienne et décimale en 6ème ?
Un QCM de maths sur la division euclidienne et décimale en 6ème.
Mathématiques Web c'est 2 207 795 fiches de cours et d'exercices téléchargées.
