Calcul littéral maths : exercices en 4ème corrigés en PDF.

Le calcul littéral et la double distributivité à travers des exercices de maths corrigés en 4ème vous sera très avantageux. Ainsi, l’élève devra être capable de simplifier et réduire une expression algébrique et connaître les règles de simplification. Il doit aussi développer une expression littérale en utilisant les propriétés de la simple et de la double distributivité. De plus, il devra aussi développer des compétences en calcul littéral à travers des exercices qui possède leur correction afin de progresser en mathématiques.

Tous ces supports sont similaires à ceux de votre manuel scolaire en quatrième.
Par ailleurs, développer un produit, c’est l’écrire sous forme de somme algébrique

Règle la distributivité
a(b + c) = ab + ac

En appliquant deux fois cette règle, on obtient : (a + b)(c + d) = ac + ad + bc + bd.

Exemples

A = (5a – 3)(3a + 2) = 5a $\times \,$ 3a + 5a $\times \,$ 2 – 3 $\times \,$ 3a – 3 $\times \,$ 2 = 15a² + 10a – 9a – 6=15a²+a-6.

Exercice n° 1 :

Ecrire de la façon la plus simple les expressions suivantes :

$a. 2\times \,3x\\ b. -3\times \,7x \\ c. 2\times \,(5x) \\ d. x\times \,7 \\ e. x\times \,(-3) \\ f. 3x\times \,(2x) \\ g. -7x\times \,(2x) \\ h. -6x\times \,(-4x)$

Exercice n° 2 :

Développer et réduire les expressions suivantes :

a .(4a + 3)(3a + 5) b. (3a – 2)(4a – 7) c. (5a + 7)(4a + 1)

d. (- 3a + 2)(5a – 4) e. (2b – 3)(2b – 7) f. (3a – 4)(4a – 11)

g. (5b – 2)(- 3b + 2) h. (3x – 4)(5x + 2) i. (- 4x + 17)(- 3x – 21)

j. (5a – 3b)(4b + 3a) k. (- a + 5b)(4b + 3a) l. (2a – b)(- 7b + 4a)

m. (3a – 3)(3a – 2) n. (3a + 2)(3a + 7) o. (2a – 7)(3a – 1)

Exercice n° 3 :

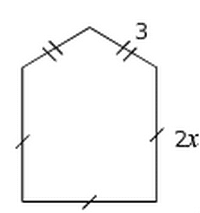
Déterminer le périmètre de la figure ci-dessous en fonction de x.

Exercice n° 4 :

En utilisant la propriété de la double distributivité, développer et réduire les expressions littérales suivantes :

A = ( x + 3 ) × (x + 1 ) B = ( x + 7 ) × ( x + 2 ) C = ( x + 2 ) ( x – 5 )

D = ( x + 3 ) ( x – 6 ) E = ( x + 6 ) ( x – 8 ) F = ( x – 3 ) ( x + 4 )

G = ( x – 7 ) ( x – 4 ) H = ( x – 1 ) ( x + 7 ) I = ( 2 x + 7 ) ( 3 x + 8 )

Exercice n° 5 :

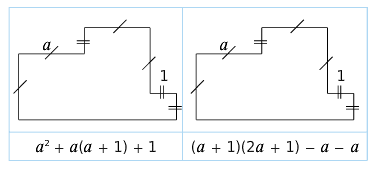
On souhaite exprimer l’aire de la figure ci-dessous, en fonction de a.

1.Voici deux propositions. Indiquer le découpage utilisé pour obtenir l’expression donnée.

2.Proposer une autre expression.

3.Montrer que les différentes expressions peuvent s’écrire 2a²+a+1.

3.4/5 - (620 votes)

Partagez

Tweetez

Enregistrer

0 Partages

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «calcul littéral : exercices en 4ème corrigés | Quatrième» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres articles analogues :

Mathématiques Web c'est 2 166 394 fiches de cours et d'exercices téléchargées.