EXERCICE 1 :
a) La fonction f est définie sur l’ensemble des nombres réels, donc elle est dérivable sur .
Sa dérivée est .
b) La fonction g est définie sur l’ensemble des nombres réels non nuls, donc elle est dérivable sur . Sa dérivée est
.
c) La fonction h est définie sur l’intervalle , donc elle est dérivable sur cet intervalle.
Sa dérivée est .
d) La fonction j est définie sur , donc elle est dérivable sur cet ensemble. Sa dérivée est
.
EXERCICE 2 :
La fonction g est définie sur l’ensemble des nombres réels, donc elle est dérivable sur .
Sa dérivée est .
Simplifiée, on obtient .
EXERCICE 3 :
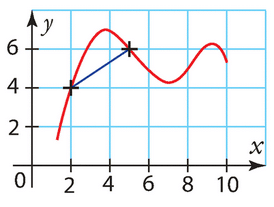
Le taux de variation de f entre 2 et 5 est donné par la formule .
D’après le graphique, on a et
.
Donc, le taux de variation de f entre 2 et 5 est .
EXERCICE 4 :
La droite passant par et
a pour coefficient directeur
. Comme la droite est tangente à la courbe en A, on a
.
EXERCICE 5 :
1. On a et
.
En utilisant l’identité remarquable , on peut écrire :
Le taux de variation de f entre 9 et est donc
.
2. Comme la limite de cette expression quand h tend vers 0 est finie, la fonction f est dérivable en 9 et sa dérivée est .
EXERCICE 6 :
On a g(3) = 6 (coordonnée y du point B).
Comme la tangente en A a pour coefficient directeur , on peut écrire :
.
Donc, g'(3) = -1.
EXERCICE 7 :
a) On peut écrire avec
et
.
Les fonctions u et v sont dérivables sur et sur
, respectivement.
La fonction somme est dérivable sur et sa dérivée est
.
b) On peut écrire avec
et
.
Les fonctions u et v sont dérivables sur et sur
, respectivement.
La fonction somme est dérivable sur et sa dérivée est
.
c) On peut écrire avec
et
.
Les fonctions u et v sont dérivables sur et la fonction somme est dérivable sur
avec
.
EXERCICE 8 :
1. L’équation de la courbe représentative de f est « ».
2. Nous plaçons un point sur la courbe en .
3. Nous traçons la tangente à la courbe en ce point.
4. Le coefficient directeur de la tangente est environ 11.
5. En plaçant le point sur les différentes valeurs de x données dans le tableau de valeurs et en traçant les tangentes, on peut estimer les valeurs approchées des dérivées demandées : .
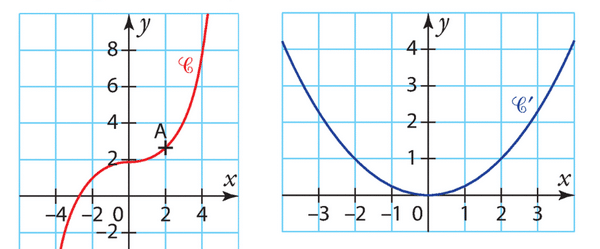
EXERCICE 9 :
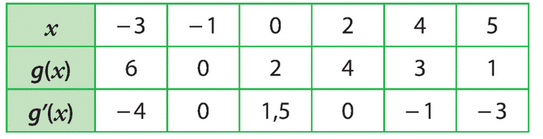
1. Les points sont .
2. En chacun de ces points, on trace la tangente à la courbe .
3. Une allure possible de est représentée ci-dessous :
Courbe à créer….
EXERCICE 10 :
Le coefficient directeur de la tangente à 6 (c’est-à-dire au point d’abscisse 2) est la valeur de la dérivée f'(2). En lisant sur le graphique, on a . Donc le coefficient directeur de la tangente à 6 est environ -2.
EXERCICE 11 :
a) La fonction f est définie pour tout x sauf 0. Donc, f est dérivable sur et sa dérivée est
.
b) La fonction g est définie pour tout x sauf 0. Donc, g est dérivable sur et sa dérivée est
.
c) La fonction h est définie pour tout x sauf 3. Donc, h est dérivable sur et sa dérivée est
.
d) La fonction j est définie pour tout x sauf 0. Donc, j est dérivable sur et sa dérivée est
.
e) La fonction k est définie sur l’intervalle ]-∞;1[ ∪ ]1;+∞[ car le dénominateur s’annule en
.
On peut factoriser en
, donc la fonction est dérivable sur cet intervalle. Sa dérivée est
.
f) La fonction m est définie pour tout x tel que , c’est-à-dire sur
.
Donc, m est dérivable sur cet intervalle et sa dérivée est .
EXERCICE 12 :
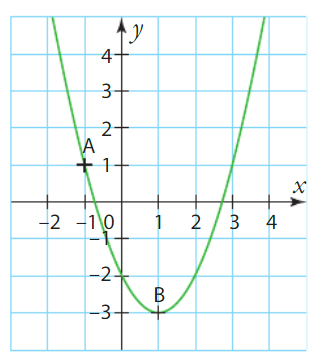
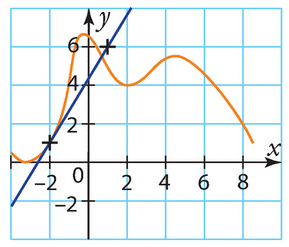
Le taux de variation de f entre -1 et 1 est donné par la formule .
D’après le graphique, on a f(-1) ≈ -6 et .
Donc, le taux de variation de f entre -1 et 1 est .
EXERCICE 13 :
On peut écrire l’égalité sous la forme : .
En simplifiant, on obtient : .
Donc, le taux de variation de f entre et
est TV = 9.
Comme ce taux ne dépend pas de h, on peut dire que la fonction f est dérivable en -7 et que .
EXERCICE 14 :
En faisant tendre x vers 3 dans l’équation , on trouve
,
donc .
Donc la fonction g est dérivable en 3 et .
EXERCICE 15 :
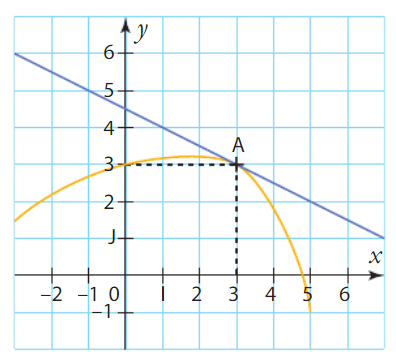
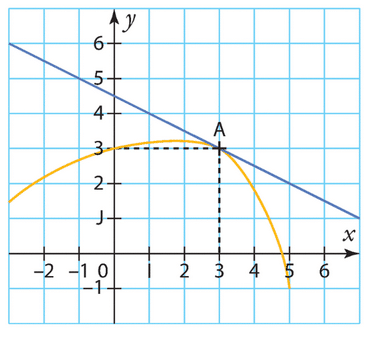
On a g(3) = 6 (coordonnée y du point B).
Comme la tangente en A a pour coefficient directeur , on peut écrire :
.
Donc, .
EXERCICE 16 :
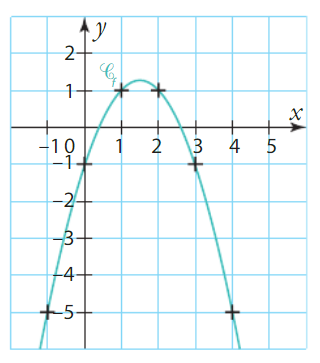
La courbe représentative est reproduite ci-dessous :
Tracer la courbe….
La tangente en 2 a pour équation , et la tangente en 0 a pour équation
.
EXERCICE 17 :
Pour les fonctions simples :
– La fonction f est dérivable sur , et sa fonction dérivée est f'(x) = 4x^3.
– La fonction g est dérivable sur , et sa fonction dérivée est g'(x) = 12x^11.
– La fonction h est dérivable sur (l’ensemble des nombres réels non nuls), et sa fonction dérivée est
.
Pour les fonctions composées :
– Pour f, on peut identifier et
.
Les fonctions u et v sont toutes deux dérivables sur R*, et donc la fonction somme f est dérivable sur R*, et sa fonction dérivée est f'(x) = -1/x^2 + 1.
– Pour g, on peut identifier u(x) = -5 et .
Les fonctions u et v sont toutes deux dérivables sur R* (avec une exception en x=0 pour v), et donc la fonction somme g est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est .
– Pour h, on peut identifier et
.
Les fonctions u et v sont dérivables sur R, et donc la fonction somme h est dérivable sur R, et sa fonction dérivée est .
EXERCICE 18 :
Pour les fonctions composées :
– Pour f, on peut identifier et
. La fonction u est dérivable sur R* (avec une exception en x=0), et la fonction v est dérivable sur R, donc la fonction produit f est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est
.
– Pour g, on peut identifier et
.
Les fonctions u et v sont dérivables sur , donc la fonction produit g est dérivable sur
, et sa fonction dérivée est
.
– Pour h, on peut identifier et
.
Les fonctions u et v sont dérivables sur R, donc la fonction produit h est dérivable sur R, et sa fonction dérivée est .
EXERCICE 19 :
1. On peut écrire . On résout l’équation
, ce qui donne
. Donc
s’annule en
.
2. Le théorème de la dérivée de l’inverse d’une fonction affirme que si f est une fonction dérivable sur un intervalle I et à valeurs dans un intervalle J, alors si g est l’inverse de f, c’est-à-dire une fonction qui vérifie pour tout x de J, alors g est dérivable sur J et sa dérivée est donnée par la formule :
.
Ici, la fonction f est dérivable sur I et à valeurs dans , donc elle est bijective sur son ensemble de définition et admet une inverse.
On peut déterminer cette inverse en résolvant l’équation en x :
on a équivaut à
, soit
, soit
.
Donc l’inverse de f est la fonction .
La dérivée de g en y est donnée par , donc
.
On peut donc exprimer en fonction de x en utilisant la formule
:
on a .
Donc f est dérivable sur I et sa dérivée est .
EXERCICE 20 :
1. On peut écrire où
et
. Donc g est définie sur
et f est dérivable sur I, donc h est définie et dérivable sur I.
2. En utilisant la formule de la dérivée d’une fonction composée, on a où
et
.
Donc .
3. On a et
pour tout x strictement positif.
4. On a donc .
EXERCICE 21 :
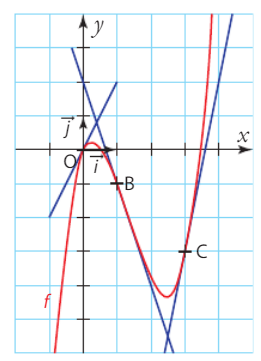
1. Graphiquement, on lit les pentes des tangentes en 0, 1 et 3 sur le graphe de f : la pente en 0 est nulle, la pente en 1 est négative et la pente en 3 est positive.
2. La tangente en C a pour coefficient directeur la dérivée en 3, soit f'(3) = 7. On utilise ensuite l’équation de la tangente en C : .
On a et donc l’équation réduite de la tangente en C est
.
3. On calcule en dérivant
terme à terme :
.
On trouve et
.
On peut vérifier que ces valeurs correspondent bien aux pentes des tangentes trouvées graphiquement. On peut également retrouver l’équation de la tangente en C en utilisant cette dérivée : et
, donc l’équation réduite de la tangente en C est
, soit
.




 Mathématiques Web c'est 2 208 799 fiches de cours et d'exercices téléchargées.
Mathématiques Web c'est 2 208 799 fiches de cours et d'exercices téléchargées.