Fractions : cours de maths en 5ème avec leçon en PDF.

Sommaire de cette fiche

Les fractions avec un cours de maths en 5ème complet pour l’élève. Cette leçon fait intervenir les notions suivantes :

définition d’un quotient et d’une fraction;
écriture fractionnaire;
règles de simplification d’une fraction;
réduction au même dénominateur;
somme de deux fractions;
différence de deux fractions;
produit de deux fractions.

L’élève devra connaître la définition d’une fraction et savoir la représenter sur une droite graduée. Il devra développer des compétences en calculs et savoir réduire deux fractions au même dénominateur afin de pouvoir les comparer. Nous terminerons ce cours sur les fractions par la résolution de problèmes en classe de cinquième.

I. Les écritures fractionnaires

1.Quotient

Définition :

On considère a et b deux nombres relatifs tel que $b\neq 0$ .

Le quotient de a par b, noté $\frac{a}{b}$ est le nombre tel que $\frac{a}{b}\times b=a$ .

Le nombre a est le numérateur de $\frac{a}{b}$ et le nombre b est le dénominateur de $\frac{a}{b}$ .

Lorsque a ou b est un nombre décimal, $\frac{a}{b}$ est appelée écriture fractionnaire.
Lorsque a et b sont des nombres entier, $\frac{a}{b}$ est appelée fraction.
Lorsque b est égal à 10,100,1 000, …, $\frac{a}{b}$ est appelée fraction décimale.

Exemple :

Le quotient de 3 par 4 est noté $\frac{3}{4}$ .

Ce nombre vérifie l’égalité $\frac{3}{4}\times 4=3$ .

Remarque :

Tout nombre décimal possède une infinité d’écritures fractionnaires.

Par exemple $3,05=\frac{3,05}{1}=\frac{30,5}{10 }=\frac{305}{100}$

2.Proportions

Exemple :

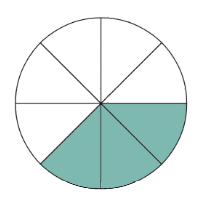
Le disque ci-dessous est divisé en six parties égales.

Chaque part représente $\frac{1}{8}$ du disque.

La proportion du disque colorié en bleue est donc $\frac{3}{8}$ .

La proportion du disque non coloriée est $\frac{5}{8}$ .

$fraction d'une fraction$

II. Les égalités de quotients et fractions

1.Quotients égaux

Propriété :

On considère a, b et k trois nombres relatifs tels que $b\neq 0$ et $k\neq 0$ .Si on multiplie (ou divise) le numérateur et le dénominateur d’un quotient par un même nombre k non nul alors on ne modifie pas la valeur du quotient.

$\frac{a}{b}=\frac{a\times k }{b\times k}=\frac{ak}{bk}$ et $\frac{a}{b}=\frac{a : k }{b : k}$ .

Exemple :

$A=\frac{0,2}{1,2}=\frac{0,2\times 5 }{1,2 \times 5}=\frac{1}{6}$

$B=\frac{24}{18}=\frac{24:6}{18:6}=\frac{4}{3}$

2.Simplifier des fractions

Propriété :

On considère a et b deux nombres entiers relatifs tel que $b\neq 0$ .

Afin de simplifier une fractions, on utilise la propriété précédente en divisant le numérateur et le dénominateur par un diviseur en commun.

Lorsque nous ne pouvons plus simplifier une fraction, celle-ci est dite irréductible.

Exemple :

$0,75=\frac{3}{4}=\frac{1,5}{2}$

Ce sont trois écritures d’un même nombre.

La première est l’écriture décimale, la seconde est une fraction et la troisième est une écriture fractionnaire.

$\frac{25}{15}=\frac{5\times 5}{5\times 3}=\frac{5}{5}\times \frac{5}{3}=1\times \frac{5}{3}=\frac{5}{3}$

Remarque :

Pour simplifier une fraction, on utilise les critères de divisibilité.

3.Division de deux nombres décimaux

Propriété :

Le quotient de deux nombres décimaux peut s’écrire sous la forme d’une fraction.

Exemple :

$9: 0,4=\frac{9}{0,4}=\frac{9\times 5}{0,4\times 5}=\frac{45}{2}$

4.Fraction décimale

Propriété :

On considère a et b deux nombres entiers relatifs tel que $b\neq 0$ .

On appelle fraction décimale, toute fraction $\frac{a}{b}$ telle que b soit égal à 10;100 ; 1 000 ; etc .

Exemple :

$\frac{5}{10};\frac{12}{100};\frac{1394}{10000}$ sont des fractions décimales.

Propriété :

Tout nombre décimal n peut s’écrire sous forme d’une fraction décimale.

Exemple :

$A=4,75=\frac{475}{100}$

5.Proportion et pourcentage

Définition :

Quand une proportion est écrite sous forme d’un quotient qui a pour dénominateur 100, nous obtenons une proportion en pourcentage.

Exemple :

une ville de 50 000 habitants est traversée par un canal.

18 250 habitants ont leur logement sur la rive droite du canal.

La proportion d’habitants ayant leur logement sur la rive droite est $\frac{18250}{50000}$ .

$\frac{18250}{50000}=\frac{18250:1000}{50000:1000}=\frac{18,25}{50}=\frac{18,25\times 2}{50\times 2}=\frac{36,5}{100}$ .

On dit que le pourcentage d’habitants ayant leur logement sur la rive droite est de 36,5 %.

III. Comparaison de fractions

Définition :

Pour comparer deux fractions, il faut préalablement, les réduire au même dénominateur puis, comparer les numérateurs.

Exemple :

Rangeons les fractions suivantes dans l’ordre croissant : $\frac{5}{7};\frac{9}{7};\frac{8}{7};\frac{4}{7}$ .

Toutes ces fractions ont pour dénominateur commun 7, elles seront rangées dans l’ordre croissant de leur dénominateur.

$\frac{4}{7}<\frac{5}{7}<\frac{8}{7}<\frac{9}{7}$ .

Remarque :

Pour comparer deux fractions qui n’ont pas le même dénominateur, on les réduit au même dénominateur puis on applique la définition précédente.

Exemple :

Comparer $\frac{4}{3}$ et $\frac{5}{4}$ .

$\frac{4}{3}=\frac{4\times 4}{3\times 4}=\frac{16}{12}$

$\frac{5}{4}=\frac{5\times 3}{4\times 3}=\frac{15}{12}$

donc

$\frac{4}{3}>\frac{5}{4}$

3.4/5 - (19 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fractions : cours de maths en 5ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 237 fiches de cours et d'exercices téléchargées.