Les nombres relatifs à travers une série d’exercices de maths en 5ème. L’élève devra connaître la définition d’un nombre relatif composé de son signe et de sa partie numérique mais, également, comparer des nombres relatifs ou les ranger dans l’ordre croissant ou décroissant. A cet effet, ces exercices lui permettront d’acquérir pour une bonne compréhension du chapitre. Par conséquent, vous retrouverez toutes les notions de ce chapitre enseignées en classe de cinquième. Des supports variés que ce soit des calculs à mener ou des problèmes concrets de la vie courante à résoudre. En effet, en classe de cinquième, nous avons appris calculer en connaissant les priorités opératoires. Vous trouverez des fiches similaires à celles que vous effectuez en classe avec votre professeur ou celles disponibles dans votre manuel scolaire (Bordas, Hachette, Sésamaths, Hatier). Ces énoncés sont corrigés et à télécharger gratuitement au format PDF.
Exercice n°1 :
Dans chacune des listes ci-dessous, quels sont les nombres relatifs positifs, négatifs, entiers ?
1) + 4 ; 0 ; – 7 ; 8,4 ; – 26 ; – 5,04 ; 0,07 ; 14
2) 8,5 ; – 1,98 ; + 19,5 ; 44 ; 0 ; – 6,1 ; – 13
Exercice n°2 :
a) Donner les abscisses des points A, E, F et I.
b) Placer les points L(– 3) ; R(– 6) et S(6).
c) Placer le point T symétrique de I par rapport à l’origine : quelle est l’abscisse de T ?
d) Quel mot peux-tu lire ? :
Exercice n°3 :
Graduer en cm une droite puis placer les points A, B, C, D, E et F d’abscisses respectives
– 2,5 ; – 3,5 ; – 2,8 ; 2,4 ; – 0,6 ; 0,6.
Exercice n°4 :
a) Tracer une droite graduée en prenant 2 cm comme unité.
b) Placer les points R et S dont les distances à zéros sont égales à 3,5.
c) Quelles sont les coordonnées de R et de S ?
d) Qui est le milieu de [RS] ?
Exercice n° 5 :
Compléter avec le symbole > , < ou =.
| 29 ….. 48
– 6 ….. 6 8 ….. 0 – 8 ….. 0 – 5 ….. – 4 – 34 ….. 24 – 18 ….. – 3 – 6,5 ….. – 9,2 |
5,27 ….. 3,58
– 5,7 ….. – 3,8 2,6 ….. – 3,8 – 4,3 ….. 2,8 – 2,5 ….. – 4,3 – 1,8 ….. – 16 – 4 236 …. 0,2 – 7,3 ….. – 4,3 |
– 15 ….. –51
3,01 …. 3,001 – 9,01 ….. – 9,9 11,09 …… 11,009 – 5,99 …… – 5,999 – 4,26 ….. – 4,3 – 23,2 ….. – 23,26 – 18,43 ….. – 18,4 |
Exercice n°6 :
Ranger dans l’ordre décroissant les nombres relatifs suivants:
3,2 ; 2,7 ; – 5,2 ; – 2,7 ; 0 ; 3,26 ; 0,8 ; – 2,72 ; – 2,08
Exercice n°7 :
a) Range dans l’ordre croissant les nombres relatifs suivants: 4,72 ; – 2,74 ; 4,702 ; – 2,704 ; 4,712 ; + 2,704
b) Range dans l’ordre décroissant les nombres relatifs suivants : – 0,8; – 0,9 ; – 0,7; 0; – 1; +1; – 0,2; + 0,6 ; – 1,3
Exercice n°8 :
Compléter les encadrements par un nombre relatif qui convient :
– 2 < ….. < 0 ; – 8,8 < ….. < – 7,7 ; – 3 < ….. < + 4 ; – 5 < ….. < – 4
– 6 < – 4 < ….. ; ….. < 2,8 < ….. ; ….. < – 26 < ….. ; – 9 < ….. < – 2
Exercice n°9 :
Quels sont les nombres entiers relatifs vérifiant : – 3 < x < + 4 et – 6 < x < – 1
Exercice n° 10 :
Déterminer la valeur des expressions suivantes :
A = (+27) – (+53) + (-2,9) – (+13,7)
B = (-25) – (-47) – (-17,7) – (+3,4)
C = (-13) – (+55) + 17 – 32 + 56 – 32 + 12,87
D = (-26 )+ (+ 75) – (+ 6) + (- 27) – (- 48)
Exercice n° 11 :
A = (+503) – (-343,8) – (-415,5) – (743,8) + (-203) + (-84,5)
Ainsi, il faut calculer A en faisant des regroupements astucieux.
Exercice n° 12 :
Simplifier puis calculer la valeur de A puis de B.
A = ( – 5 ) + ( 3 – 2 x 4 – 6) – ( – 12 )
B = (+ 7,4) – [2 + ( 3 – 4 x 2,6)]+ (-7) + (-11)
Exercice n° 13 :
Ramsès II fut un pharaon né en -1304.Il a vécu 67 ans.
Ramsès III a vécu 32 ans et s’est éteint en -1134.
Combien d’années séparent la date de décès de Ramsès II de la date de décès de Ramsès III ?
Exercice n° 14 :
Calculer chaque expression.
Exercice n° 15:
Calculer chaque expression.
Exercice n° 16 :
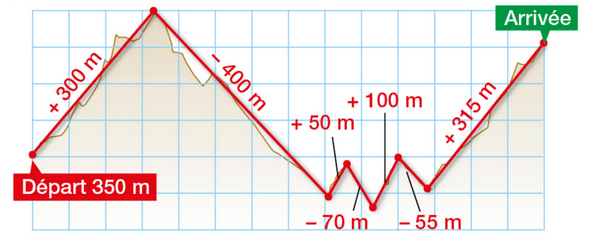
Lilian s’est inscrit au « Trail de la Galinette », une course qui débute à Cadolive (Bouches-du-Rhône). Quelques jours avant le départ, il étudie le graphique des dénivelés.
a. Ecrire une expression qui permet de calculer l’altitude à l’arrivée.
b. Calculer cette altitude.
Exercice n° 17 :
Calculer astucieusement.
Exercice n° 18 :
Calculer à la main.
Exercice n° 19 :
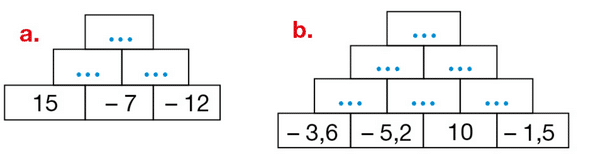
Dans chaque brique, le nombre à inscrire est la somme des nombres notés dans les deux briques
situées en dessous.
Recopier et compléter chaque pyramide.
Exercice n° 20 :
Calculer à la main.
Exercice n° 21 :
Thalès est né en -625 et mort en -546.
Pythagore est né en -580 et mort en -495.
Hypatie est née en 355 et morte en 415.
Lequel de ces trois philosophes et mathématiciens a vécu le plus longtemps ?
Exercice n° 22 :
Calculer à la main.
Exercice 23 :
Ranger les nombres relatifs suivants dans l’ordre croissant.
Exercice 24 :
Ranger par ordre décroissant ces grandes dates de la civilisation romaine.
Exercice 25 :
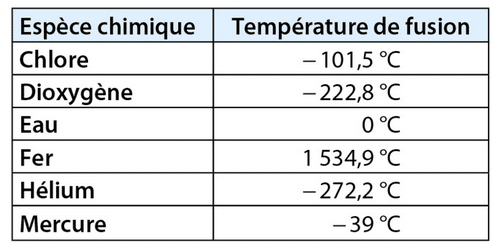
La fusion est le passage de l’état solide à l’état liquide.
Voici la température de fusion de certaines espèces chimiques.
Ranger ces températures de fusion dans l’ordre croissant.
Exercice 26 :
Associer chaque thermomètre (en °C) à la phrase correspondante.
Expliquer.
Exercice 27 :
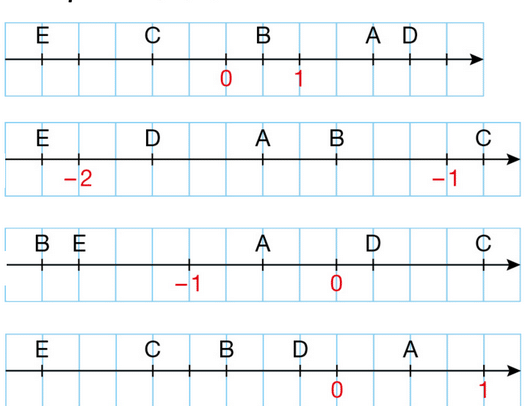
Donner l’abscisse de chacun des points A, B, C, D et E.
Exercice 28 :
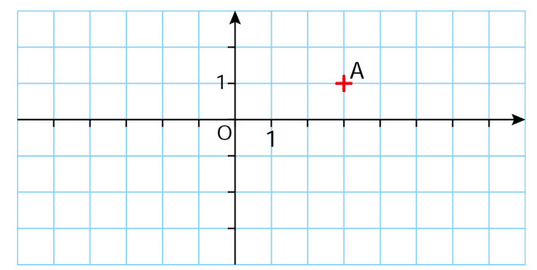
1. Donner les coordonnées du point A dans le repère ci-dessous.
2. Reproduire cette figure et représenter:
a. En vert, les points qui ont la même abscisse que A ;
b. En bleu, les points qui ont la même ordonnée que A.
Exercice 29 :
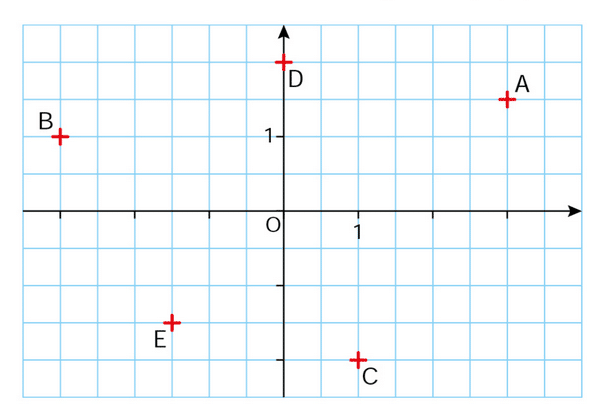
Donner les coordonnées des points A, B, C, D et E.
Exercice 30 :
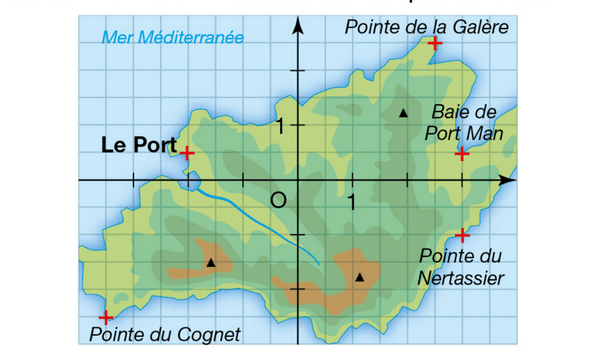
Corentin et Sarah organisent une randonnée à Port-Cros (dans le Var) afin de faire le tour de l’île. Les lieux indiqués sur la carte correspondent aux différents points d’arrêt pendant leur parcours.
Déterminer les coordonnées de ces points d’arrêt.












 Mathématiques Web c'est 2 208 798 fiches de cours et d'exercices téléchargées.
Mathématiques Web c'est 2 208 798 fiches de cours et d'exercices téléchargées.
Bonjour,
Je suis papa d’un enfant de 5ème vos exercices sont très intéressants pour les révisions avec ma fille. Néanmoins, je ne trouve pas le lien pour le téléchargement du format PDF ? Pouvez vous svp nous indiquer comment télécharger ces exercices en pdf pour les imprimer ?
Cordialement
bonjour
le lien pour télécharger en PDF est toujours situé à la fin de la série d’exercices.