Théorème de Pythagore: cours de maths en 4ème en PDF.

Sommaire de cette fiche

Le théorème de Pythagore avec un cours de maths en 4ème sur la définition de l’hypoténuse dans un triangle rectangle est toujours nécessaire. L’élève devra maîtriser la partie directe et la partie réciproque du théorème. De plus, il va développer des compétences de calcul en déterminant la longueur des côtés et avoir assimilé la signification concrète du théorème de Pythagore au point de vue géométrique avec des aires de carrés en quatrième. Ce théorème est fondamental au collège et son utilisation sera récurrente tout au long de votre scolarité.

I. Vocabulaire du triangle rectangle

Définition :

Un triangle rectangle est un triangle qui possède un angle droit;
Le coté le plus long d’un triangle rectangle, qui est le côté opposé à l’angle droit, s’appelle l’hypoténuse.

Exemple :

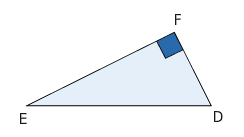
DEF est un triangle rectangle en F;
[ED] est l’hypoténuse : c’est le plus long côté du triangle rectangle;
Les deux côtés adjacents à l’angle droit sont [FD] et [FE], ils sont perpendiculaires.

II. Partie directe du théorème de Pythagore

1.Théorème de Pythagore

Théorème :

Si un triangle est rectangle alors le carré de l’hypoténuse est égal à la somme des carrés des longueurs des côtés adjacents à l’angle droit.

Exemple :

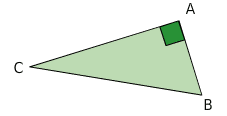
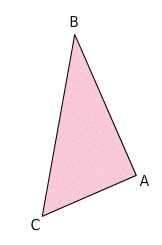
ABC est un triangle rectangle en A donc d’après la partie directe du théorème de Pythagore,

nous avons : .

2. Calcul de la longueur de l’hypoténuse

Exemple :

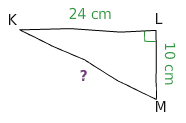
Soit KLM un triangle rectangle en L tel que KL = 24 cm, LM = 10 cm.

Calculer KM.

Le triangle KLM est rectangle en L donc d’après la partie directe du théorème de Pythagore, nous avons l’égalité suivante :

$KM^2=KL^2+LM^2\\KM^2=24^2+10^2\\KM^2=576+100\\KM^2=676\\KM=\sqrt{676}\\KM=24\,cm$

3. Calcul de la longueur d’un côté adjacent à l’angle droit

Exemple :

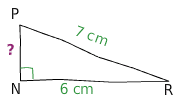
Soit NPR un triangle rectangle rectangle en N tel que PR = 7 cm et Nr = 6 cm.

Calculer NP (arrondir le résultat au dixième).

Le triangle PNR est rectangle donc d’après la partie directe du théorème de Pythagore,

nous avons l’égalité suivante :

$PR^2=PN^2+NR^2\\7^2=PN^2+6^2\\49=PN^2+36\\PN^2=49-36\\PN^2=13\\PN=\sqrt{13}\\PN\approx 3,6\,cm$

4. Démontrer qu’un triangle n’est pas rectangle

Exemple :

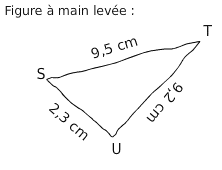
Soit STU un triangle rectangle en U tel que ST = 9,5 cm; Su = 2,3 cm et UT = 9,2 cm.

Le plus grand côté est [ST].

Je calcule séparément :

$ST^2=9,5^2=90,25\,cm^2$

$SU^2+UT^2=2,3^2+9,2^2=5,29+84,64=89,93\,cm^2$

$ST^2\neq SU^2+UT^2$ donc le triangle SUT n’est pas rectangle.

III. Partie réciproque du théorème de Pythagore

1. Réciproque du théorème de Pythagore

Théorème :

Si, dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés alors ce triangle est rectangle.

Exemple :

ABC est un triangle tel que . Donc, d’après la partie réciproque du théorème de Pythagore, on en déduit que le triangle ABC est rectangle en A.

2. Démontrer qu’un triangle est rectangle

Exemple :

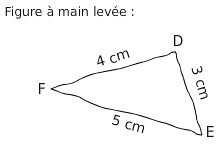
Soit DEF un triangle tel que FD = 4 cm; FE = 5 cm et DE = 3 cm.

Le côté le plus long est [FE].

Je calcule séparément :

$FE^2=5^2=25\,cm^2\\ FD^2+DE^2=4^2+3^2=16+9=25\,cm^2$

donc le triangle FED est rectangle en D.

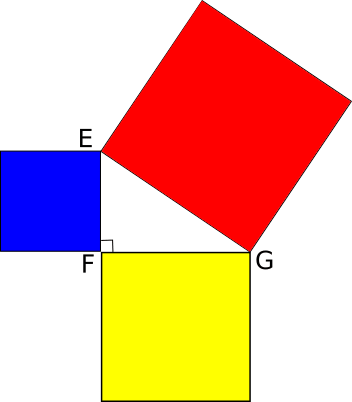
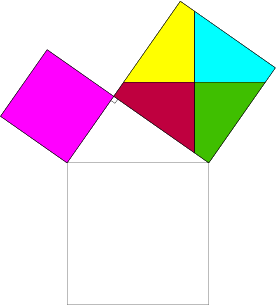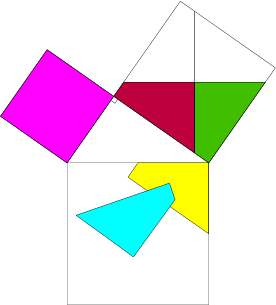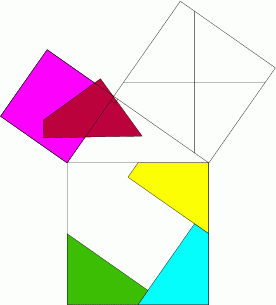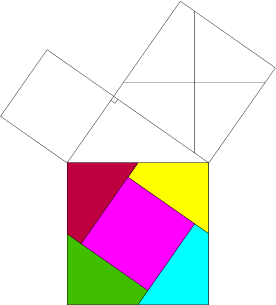
IV. Signification géométrique du théorème de Pythagore

Propriété :

Si DEF est un triangle rectangle en F alors DE²=EF²+DF².

${\color{Red} Aire_{carre-rouge}}={\color{Blue} Aire_{carre-bleu}}+{\color{Yellow} Aire_{carre-jaune}}$

Application :

Une chèvre C est attachée à un piquet P planté au coin d’un pré carré de 15 m de côté.

Quelle doit être, approximativement, la longueur de la corde pour que la chèvre puisse brouter tout le pré?

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «théorème de Pythagore : cours de maths en 4ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.