sommaire
Nous terminerons cette leçon en résolvant des problèmes de la vie courante en troisième.
I. La partie directe du théorème :
1.Le théorème de Thalès :
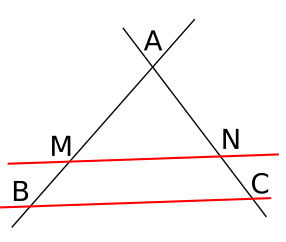
On considère une configuration de Thalès.
Si on a :
;
alors nous avons les égalités des rapports suivantes :
.
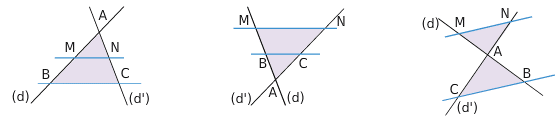
Trois configurations illustrent le théorème de Thalès dites du « triangle », du « sablier », du « huit ».
Remarque :
Les longueurs du triangle AMN sont proportionnelles aux longueurs du triangle ABC.
2.Calculs de longueurs :
Exemple :
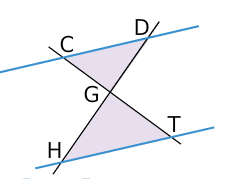
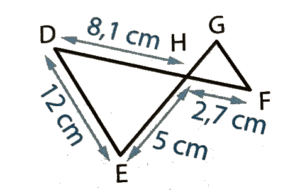
La figure ci-dessus est composée de quatre droites.
Les droites bleues sont parallèles.
DG=25 mm, GH=45 mm, CG = 20 mm, HT = 27 mm.
Les droites (DH) et (CT) sont sécantes en G.
Les droites (CD) et (HT) sont parallèles.
D’après la partie directe du théorème de Thalès, on a les égalités suivantes :
soit .
Calcul de GT :
Calcul de CD :
3.Démontrer que deux droites ne sont pas parallèles :
Exemple :
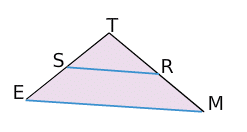
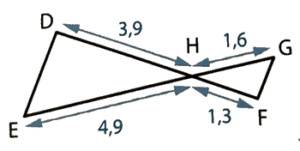
Ci-dessus, les droites (ES) et (MR) sont sécantes en T.
TR= 11 cm; TS = 8 cm; TM = 15 cm et TE= 10 cm.
D’une part, .
On constate que .
Or, si les droites (RS) et (ME) étaient parallèles, d’après le théorème de Thalès, il y aurait égalité.
Comme ce n’est pas le cas, les droites (RS) et (ME) ne sont pas parallèles.
II. Le théorème réciproque :
Réciproque du théorème de Thalès :
Si les points A,N,C sont alignés dans le même ordreet si nous avons :
alors .
Remarque :
Attention, il ne suffit pas de vérifier l’égalité des rapports : il faut aussi s’assurer que les points sont bien placés dans le bon ordre.
2.Démontrer que deux droites sont parallèles :
Exemple :
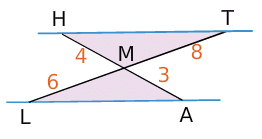
Ci-dessus, les droites (HA) et (TL) sont sécantes en M.
D’une part, , d’autre part .
On constate que .
De plus, les points A,M,H d’une part et les points M,L,T d’autre part sont alignés dans le même ordre.
Donc, d’après la réciproque du théorème de Thalès, les droites (AL) et (HT) sont parallèles.
Avez-vous assimilé ce cours sur ce théorème en 3ème ?
QCM sur le théorème de Thalès en 3ème.
Mathématiques Web c'est 2 207 984 fiches de cours et d'exercices téléchargées.
