Un devoir surveillé de mathématiques sur le théorème de Thalès en troisième (3ème).
Ce contrôle de maths sur le théorème de Thalès est destiné aux enseignants, mais également aux élèves désireux de réviser un devoir surveillé de mathématiques sur le théorème de Thalès. A la fin de ce contrôle, vous devriez assimiler des compétences nouvelles. Utilisez les matériels nécessaires pour résoudre les exercices.
Exercice n° 1 :
Tracer un triangle ABC tel que :
AB = 6 cm, AC = 4,8 cm et BC = 8,4 cm
Sur [BA), placer le point E tel que BE = 11 cm.
Sur [CA), placer le point F tel que CF = 8,8 cm.
1) Calculer AE et AF.
2) Démontrer que (EF) // (BC).
3) Calculer la longueur du segment [EF] .
Exercice n° 2 :
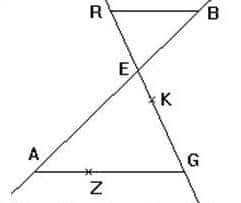
Sur la figure, les droites (AG) et (RB) sont parallèles. L’unité de longueur est le centimètre.
On a : BE = 3, AE = 5, AG = 10 et EG = 8.
1) Calculer les distances RB et RE.
2) On donne GK = 6,4 et GZ = 8.
Les droites (ZK) et (AE) sont-elles parallèles ?
Exercice n° 3 :
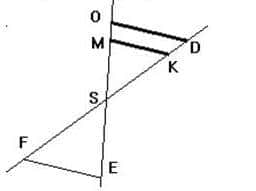
Sur la figure :
– Les droites (MK) et (OD) sont parallèles ;
– Les points E, S, M et O sont alignés dans cet ordre ;
– Les points F, S, K et D sont alignés dans cet ordre;
– SO = 6 ; SD = 10 ; SM = 4,8 ;SE = 2 et SF = 3.
1) Calculer SK.
2) Les droites (EF) et (OD) sont-elles parallèles ?
Justifier.
Exercice n° 4 :
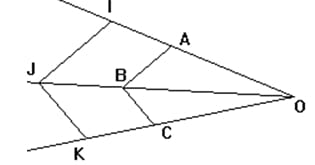
Sur la figure ci-dessous, on a :
(AB) // (IJ) et (BC) // (JK) ;
OA=3 cm ; OB=3,5 cm ; OC=2,5 cm et CK=1 cm.
1) Calculer OJ, BJ, OI et IA.
2) Les droites (AC) et (IK) sont-elles parallèles ?
Justifier.





 Mathématiques Web c'est 2 209 063 fiches de cours et d'exercices téléchargées.
Mathématiques Web c'est 2 209 063 fiches de cours et d'exercices téléchargées.