Vecteurs et repérage dans le plan et translation : cours en 2de en PDF.

sommaire

1 I. Notion de vecteur et translation
2 II. Coordonnées dans un repère orthonormé du plan

Les vecteurs et la translation avec un cours de maths en 2de où nous reverrons le repérage dans le plan et les coordonnées dans un repère orthonormé ainsi que les coordonnées d’un vecteur.

A la fin de cette leçon, l’élèves devra avoir acquis les savoir-faire suivants :

Savoir calculer la longueur d’un segment dans un repère orthonormé;
Savoir déterminer les coordonnées du milieu d’un segment;
Savoir déterminer si deux vecteurs sont égaux avec ou sans coordonnées;
Savoir déterminer, demander, affecter une valeur et afficher une variable dans un algorithme.
Milieu d’un segment;
Distance entre deux points ou norme d’un vecteur du plan;
Egalité de vecteurs (coordonnées, parallélogramme, vecteurs et milieu) en seconde.

I. Notion de vecteur et translation

1.Translation de vecteur $\vec{AB}$

Définition :

Soient A et B deux points du plan.

La translation qui transforme A en B associe à tout point du plan C le point D tel que les segments [AD] et [BC] aient le même milieu.

On l’appelle la translation de vecteur $\vec{AB}$ , souvent notée $t_{\vec{AB}}$ .

Remarque :

Le quadrilatère ABDC est alors un parallélogramme, éventuellement aplati.

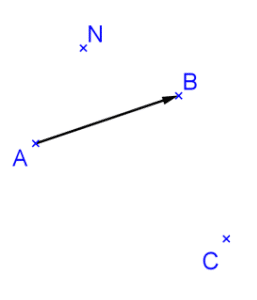
Construire l’image du point C et celle du point N par la translation de vecteur $\vec{AB}$ .

2. Vecteurs égaux

Définition :

Deux vecteurs $\vec{AB}$ et $\vec{CD}$ sont égaux si la translation qui transforme A en B transforme également C en D.

On note $\vec{AB}=\vec{CD}$ .

Propriété :

Deux vecteurs et sont égaux si et seulement si le quadrilatère ABDC est un parallélogramme, éventuellement aplati.

3.Représentant d’un vecteur

Définition :

La translation de vecteur $\vec{AB}$ transforme aussi C en D, E en F.

On a $\vec{AB}=\vec{CD}=\vec{EF}$ .

Ils sont les représentants d’un même vecteur, que l’on peut noter $\vec{u}$ par exemple.

4.Vecteurs particuliers

Définitions :

Le vecteur nul, associé à la translation qui transforme A en A, B en B, C en C….

Nous avons $\vec{AA}=\vec{BB}=\vec{CC}=\vec{0}$

Le vecteur opposé au vecteur $\vec{AB}$ est le vecteur associé à la translation qui

transforme B en A : c’est le vecteur $\vec{BA}$ .

Nous avons $\vec{BA}=-\vec{AB}$ .

Définition du milieu d’un segment :

Le point I est le milieu du segment [AB], si et seulement si, $\vec{AI}=\vec{IB}$ .

II. Coordonnées dans un repère orthonormé du plan

Dans un repère orthonormé du plan $(O,\vec{i},\vec{j})$ , on considère un vecteur $\vec{u}$ et M l’image du point O par la translation de vecteur $\vec{u}$ .

1.Définition et propriétés

Définition :

Les coordonnées du vecteur $\vec{u}$ sont les coordonnées du point M tel que :

$\vec{OM}=\vec{u}$ .

On note $\vec{u}(x;y)$ ou $\vec{u},(\,x;y\,\,)$ .

Remarque :

Le vecteur nul a pour coordonnées $\vec{0}(0;0)$ .

Propriété :

Deux vecteurs sont égaux si et seulement si ils ont les mêmes coordonnées dans le même repère.

2.Coordonnées d’un vecteur dans le plan

Définition :

Dans un repère orthonormé du plan, Soient A et B les points de coordonnées et .

Les coordonnées du vecteurs coordonnées du $\vec{AB}$ sont $\vec{AB}(x_B-x_A;y_B-y_A)$ .

3.Norme d’un vecteur.

Définition :

La norme d’un vecteur $\vec{u}$ est la longueur du vecteur $\vec{u}$ que l’on note $\,||\vec{u\,}||$ .

Dans un repère orthonormé du plan :

Si $\vec{u}(x;y)$ alors $||\vec{u\,}||=\sqrt{x^2+y^2}$ .

Remarque :

Cette égalité provient du théorème de Pythagore.

4. Distance entre deux points ou longueur d’un segment

Propriété :

Dans un repère orthonormé du plan.

Si et alors $||\vec{AB\,}||=\sqrt{,(x_B-x_A\,)^2+(y_B-y_A)^2}$ .

5.Coordonnées du milieu d’un segment

Propriété :

Le point I est le milieu du segment [AB] a pour coordonnées :

$I(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}})$

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «vecteurs et repérage dans le plan et translation : cours de maths en 2de en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 078 fiches de cours et d'exercices téléchargées.

I. Notion de vecteur et translation

1.Translation de vecteur <img decoding="async" class="LatexImg" src="https://mathematiques-web.fr/cgi-bin/mimetex.cgi?\vec{AB}" alt="\vec{AB}" alt="\vec{AB}" />

2. Vecteurs égaux

3.Représentant d’un vecteur

4.Vecteurs particuliers

II. Coordonnées dans un repère orthonormé du plan

1.Définition et propriétés

2.Coordonnées d’un vecteur dans le plan

3.Norme d’un vecteur.

4. Distance entre deux points ou longueur d’un segment

5.Coordonnées du milieu d’un segment

Réviser les cours et exercices avec nos Q.C.M :

D'autres ressources pour progresser en autonomie :

1.Translation de vecteur $\vec{AB}$